What Is the Golden Ratio?
Mathematicians and physicists will often use mathematics to help them understand the world around them and to find out how things work. Wherever we look, we can see examples of mathematics from Pythagoras to Algebra and Pi. Another example is the golden ratio that is commonly found in the natural world.
The golden ratio is closely linked with the Fibonacci sequence but they are not exactly the same thing. The chances are that there is an example of the golden ratio close to you right now. Here’s a look at what it is and where you can expect to find it.

1. The Golden Ratio
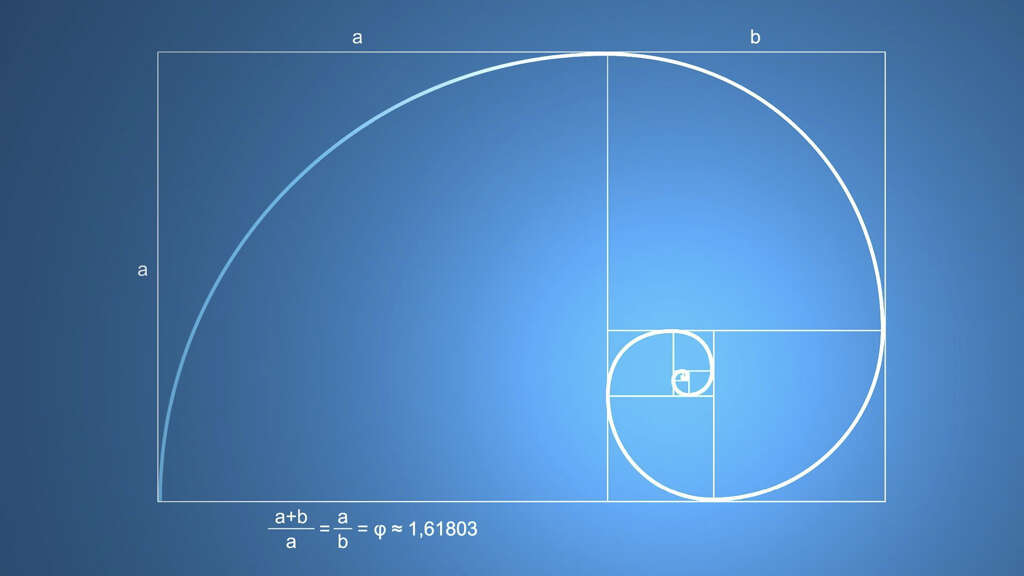
The golden ratio is a mathematical observation of a phenomenon that occurs regularly in the natural world. The ratio is a number that is found when you divide a line in two parts. The number is found when the longer part of the line divided by the smaller part equals the length of the whole line. The mathematical symbol for the golden ratio is (phi), which is the 21st letter of the Greek alphabet.
The mathematical formula for the golden ratio is a/b = (a+b)/a = 1.6180339887498948420. It also has other names including, but not limited to, the golden mean, medial section, divine section, golden proportion, and golden section.

2. The Fibonacci Sequence
The Fibonacci sequence is named after the Italian mathematician, Leonardo Fibonacci, who is credited with writing about the phenomenon. The sequence goes that each number in the sequence is the sum of the two numbers preceding it. For example, the fourth number is 5 because the previous two numbers were 2 and 3.
The golden ratio and the Fibonacci are not the same thing, but the two are still closely related. Take any two numbers in the Fibonacci sequence and the number will always be close to the golden ratio. What’s more is that the higher up the Fibonacci sequence you go, the closer the number will be to the golden ratio.
3. Shells
One of the best examples of the golden ratio occurring in nature is in shells, particularly snail shells. Take a cross section of a shell and you will be able to see that it has a spiral shape, with the spiral becoming wider as the shell grows larger.
If you were to draw a rectangle around this spiral at any point then you will find that the ratio of the sides of the rectangle is equal to the golden ratio. This will continue to be true no matter how small the shell is, or how large it grows. It also applies to the shells of many other shelled species.

4. Human Face
The golden ratio can even be found in our own faces. For example, we find the golden ratio in the distances between our pupils, teeth, and chin, giving us a ratio of approximately 1.634. Another example is the distance from our hairline to our eyebrow and eye (approximately 1.605).
Of course, we all have different facial characteristics so these values will vary from person to person but it is still clear to see the golden rule in action and the averages get increasingly closer to with the more measurements we take. In addition, those with features that are closer to the golden rule are also often considered to be among the most attractive.

5. Flower Petals
Flowers are another example of how nature can be beautiful. They can help to brighten up the home and can also help to brighten up somebodys day. They can also smell wonderful. In addition, you will find examples of the golden rule when it comes to petals.
One of the best examples of this is in the lily, which has 3 petals. A buttercup, which is common in meadows and other grassy areas, have 5 petals, whereas daisies have 34. These arrangements are down to a result of evolution and optimizing the plants exposure to the sun so they can photosynthesize.

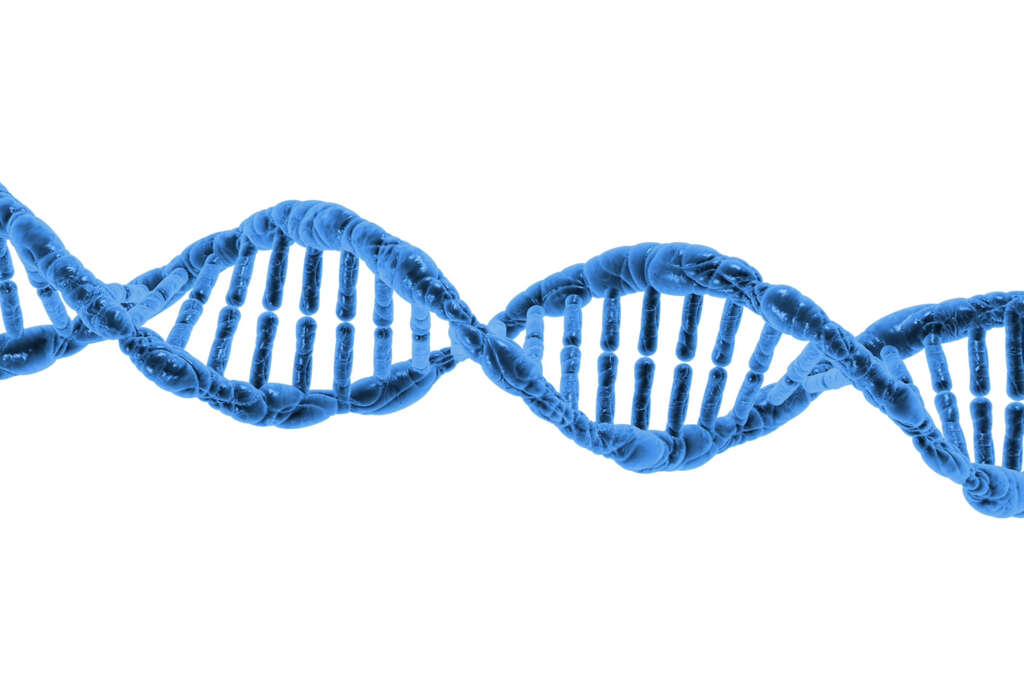
6. DNA
Our DNA contains the blueprints for just about everything about us. It determines, for example, how tall we are, the color of our eyes, and the color of our hair. It even determines many aspects of our personalities. DNA is passed on to children from both parents, meaning children share the characteristics of both.
A DNA molecule is 34 angstroms (a unit of length) long while, for every full cycle of its double helix, it is also 21 angstroms wide. The ratio of the numbers is close to at 1.6190476. Both of these numbers are also consecutive numbers in the Fibonacci sequence.
7. Spiral Galaxies
Our planet is located in the Milky Way, which is the name of our particular galaxy. When the conditions are right and there is no light pollution, we are able to see the rest of our galaxy quite clearly in the night sky. There are other galaxies and these make up some of the lights that we see in the sky.
Galaxies come in different shapes and sizes and our galaxy, along with many others, has a spiral shape. As with so many other natural formations, you will also find examples of the golden ratio in the shape and pattern of spiral galaxies.

8. Seed Heads
Plants reproduce first by being pollinated from another plant and then growing seeds to be dispersed. Different plants have different methods of dispersion, including passing through the digestive systems of animals and seed cases that have evolved to be carried long distances on the wind.
In some plants, such as in sunflowers, the seeds will grow at the head of the plant. The seeds tend to grow in large numbers and will often form spiral patterns. These patterns will often follow the golden ratio. In addition, when counting the spirals, you will find examples of the Fibonacci sequence as well.

9. Reproduction
All animals reproduce as a way of continuing the passing on of genetic information. Some have rather different methods of procreation than others but the end result is essentially the same.
Some species will give birth to relatively few offspring with a focus on helping individuals survive, whereas others will give birth to many, giving them relative safety in numbers. The golden ratio can even be seen in reproduction patterns. In honey bees, for example, the number of grandparents that male bees have follows the Fibonacci sequence and, by extension, the golden ratio. In addition, there are always more females than males in a colony, and the ratio between the two is close to .

10. Architecture
While many examples of the golden ratio are found in nature, this is not always the case. Some examples are manmade, particularly in some of our buildings. One such example is the Great Pyramids of Egypt, which are the burial places of kings and queens of ancient Egyptian civilizations.
If you were to draw a vertical line up the center of one of the pyramids and then halve the square base, you get a ratio of 1.62. The golden ratio is also found in other architecture including New York’s UN building, the Notre Dame in Paris, and Indias famous Taj Mahal.












